Topology Rubber Sheet Geometry

We can imagine the.

Topology rubber sheet geometry. An entry level primer on rubber sheet geometry. Recalling that the topology defines the structure of the space it is the topology that is keeping the sphere together. This theorem of euler is a result in topology a subject which tries to find those properties of geometrical objects that are invariant under continuous deformation a tetrahedron can be changed in this way into a cube. Math 560 introduction to topology what is topology.

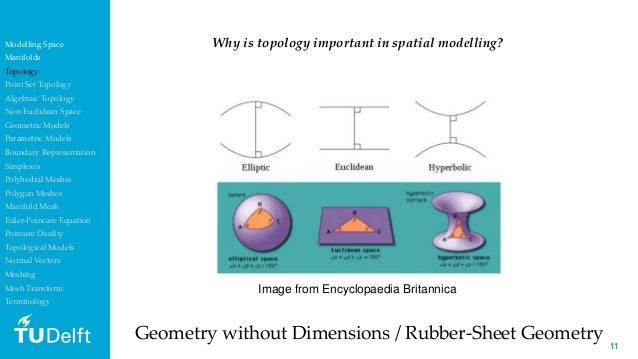
Topology studies properties of spaces that are invariant under any continuous deformation. A circle made out of a rubber band can be stretched into a square. For example a square can be deformed into a circle without breaking it but a figure 8 cannot. A möbius strip a surface with only one side and one edge.

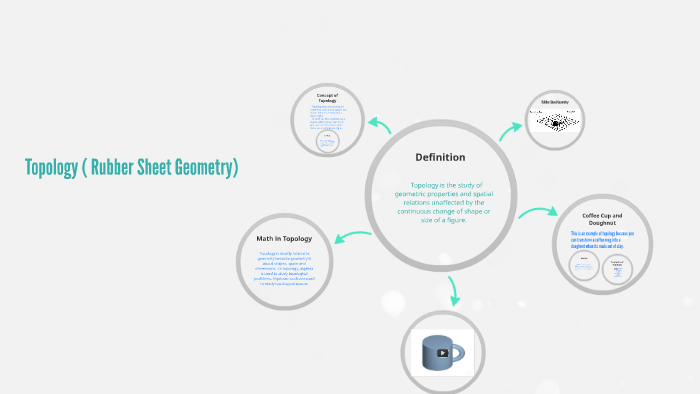
Topology has been called rubber sheet geometry. Topology has sometimes been called rubber sheet geometry because it does not distinguish between a circle and a square a circle made out of a rubber band can be stretched into a square but does distinguish between a circle and a figure eight you cannot stretch a figure eight into a circle without tearing. Topology or rubber sheet geometry topology is a branch of mathematics that deals with the ways in which figures can be distorted by stretching shrinking twisting or bending without changing certain basic properties. Topology is sometimes called rubber sheet geometry.

Topology branch of mathematics sometimes referred to as rubber sheet geometry in which two objects are considered equivalent if they can be continuously deformed into one another through such motions in space as bending twisting stretching and shrinking while disallowing tearing apart or gluing together parts. In a topology of two dimensions there is no difference between a circle and a square. It is sometimes called rubber sheet geometry because the objects can be stretched and contracted like rubber but cannot be broken. Such shapes are an object of study in topology.